Comment une particule chargée électriquement se comporte-t-elle dans les champs électriques et magnétiques?

Une particule chargée électriquement est une particule,qui a une charge positive ou négative. Il peut s'agir à la fois d'atomes, de molécules et de particules élémentaires. Quand une particule électriquement chargée est dans un champ électrique, la force de Coulomb agit sur elle. La valeur de cette force, si la valeur de l'intensité du champ à un point particulier est connue, est calculée par la formule suivante: F = qE.

Et ainsi,

nous avons déterminé qu'une particule électriquement chargée qui se trouve dans un champ électrique se déplace sous l'influence de la force de Coulomb.

Considérons maintenant l'effet Hall. Il a été trouvé expérimentalement qu'un champ magnétique affecte le mouvement des particules chargées. L'induction magnétique est égale à la force maximale, qui affecte la vitesse d'une telle particule du côté du champ magnétique. La particule chargée se déplace à une vitesse unitaire. Si une particule chargée électriquement vole dans un champ magnétique à une vitesse donnée, alors la force agissant du côté du champ sera perpendiculaire à la vitesse de la particule et, par conséquent, au vecteur d'induction magnétique: F = q [v, B]. Puisque la force qui agit sur la particule est perpendiculaire à la vitesse du mouvement, l'accélération donnée par cette force est également perpendiculaire au mouvement, c'est l'accélération normale. En conséquence, la trajectoire rectiligne du mouvement sera courbée lorsqu'une particule chargée frappe le champ magnétique. Si la particule vole parallèlement aux lignes d'induction magnétique, le champ magnétique n'agit pas sur la particule chargée. Si elle vole perpendiculairement aux lignes d'induction magnétique, alors la force qui agit sur la particule sera maximale.

Maintenant nous écrivons la loi de II Newton: qvB = mv²/ R, ou R = mv / qB, où m est la masse de la chargeparticule, et R est le rayon de la trajectoire. De cette équation, il s'ensuit que la particule se déplace dans un champ uniforme le long de la circonférence du rayon. Ainsi, la période de révolution d'une particule chargée le long d'un cercle ne dépend pas de la vitesse du mouvement. Il convient de noter que les particules électriquement chargées piégées dans le champ magnétique, l'énergie cinétique est inchangé. Étant donné que la force est perpendiculaire au mouvement des particules dans l'un des points de la trajectoire, la force du champ magnétique qui agit sur la particule ne réalise pas le travail associé à déplacer la particule chargée.

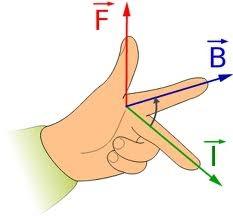
La direction de la force agissant sur le mouvementparticule chargée dans un champ magnétique, peut être déterminée en utilisant la «règle de la main gauche». Pour cela, il est nécessaire de positionner la main gauche de telle sorte que quatre doigts pointant direction de la vitesse d'une particule chargée, puits et les lignes d'induction magnétique sont dirigés dans le centre de palme, dans ce cas, plié à 90 degrés pouce indique la direction de la force qui agit sur le positif particule chargée. Dans le cas où la particule a une charge négative, la direction de la force sera opposée.

Si une particule chargée électriquement tombela région d'action conjointe des champs magnétiques et électriques, alors une force appelée force de Lorentz va agir sur elle: F = qE + q [v, B]. Le premier terme dans ce cas se réfère au composant électrique, et le second au composant magnétique.